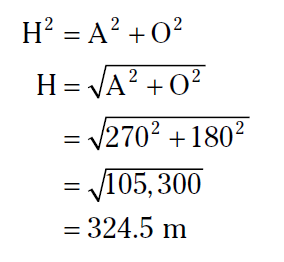۲/۸ - حقه های مثلثاتی
مثلثات یک رشته از ریاضی است که رابطه بین طرف و زاویه مثلثات را شرح میده. مثل قضیه فیثاغورس، بهتون اجازه میده تا طول نا معلوم یک مثلث قائم الزاویه رو حساب کنید. توابع مثلثاتی، جعبه ابزار شما برای کار با مثلث های قایم الزاویه هستند.
تعریف توابع مثلثاتیتوابع مثلثاتی رابطه بین دو سمت یک مثلث قائم الزاویه رو مشخص میکنه. اینها دو تا مقدار قابل اندازه گیری هستن که به این شکل نوشته میشن:
رابطه یا نرخ = یک اندازه گیری تقسیم بر اندازه گیری دیگر
یا برای مثلث قائم الزاویه:
تابع مثلثاتی = طول یک سمت تقسیم بر طول دیگر
این رابطه ها، توابع مثلثاتی نامیده میشن چون رابطه بین طول های یک مثلث قائم الزاویه، به اونا بستگی داره، یا تابع اندازه یک زاویه حاد خاص هستن.
سه تابع مثلثاتی مورد علاقه، سینوس، کسینوس، و تانژانت هستن. شکل ۲-۲ رو یه باره دیگه نگاه کنید تا توابع مثلثاتی رو بر اساس اون بهتون بگم:
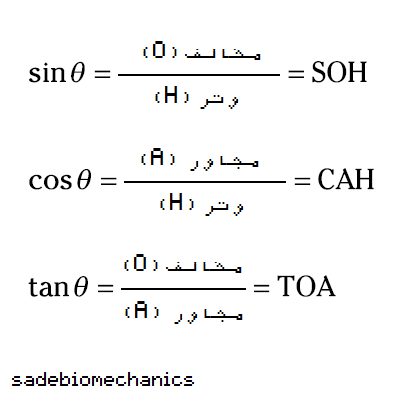
هر تابع مثلثاتی، رابطه بین دو سمت یه مثلث قائم الزاویه به صورت تابعی از زاویه تتا میگن. مثلا در مورد سینوس، میشه گفت که سینوس تابع، رابطه بین سمت مخالف و وتر رو به عنوان تابعی از زاویه تتا، مشخص میکنه. رابطه بین سمت مخالف و وتر، همیشه برای یک زاویه، یکیه و فرقی نمیکنه که تلاشن چقدر باشه. برای باقی توابع هم این موضوع صدق میکنه.
میتونین این سه تابع مثلثاتی رو به صورت SOH, CAH, TOA حفظ کنید.
استفاده از توابع مثلثاتی برای محاسبه طول
یک قائم الزاویه با وتر ۱۵ متری و یک زاویه حاد ۷۴ درجه در شکل ۳-۲ نشان داده شده. برای محاسبه سمت مجاور و مخالف، این مراحل را طی کنید:
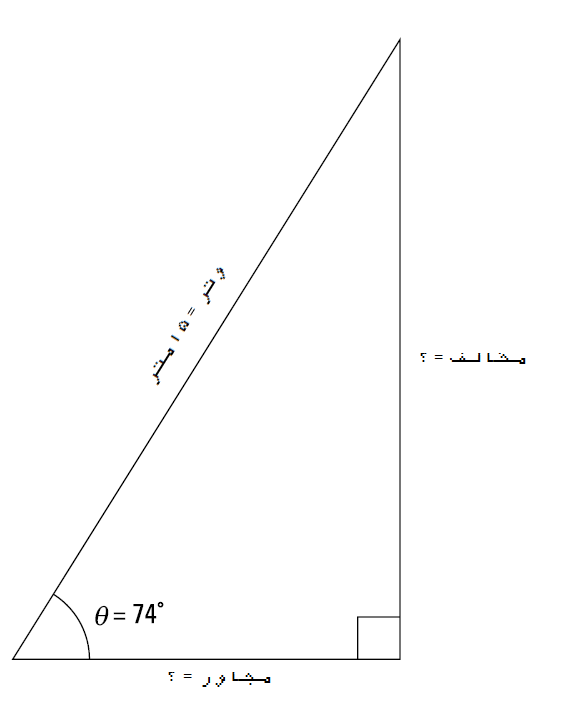
۱. مقادیر معلوم رو مشخص و یک جدول متغیری درست کنید.
تتا = ۷۴ درجه
وتر (H) = پانزده متر
سمت مجاور = نا معلوم
۲. تابع مثلثاتی برای استفاده رو مشخص کنید.
SOH CAH TOA رو یادتونه؟ بینیم هر کدوم چی لازم دارن.
SOH به زاویه تتا احتیاج داره، که میدونین، همچنین وتر که اونم میدونین و سمت مخالف که نمیدونین. پس از SOH نمیشه استفاده کرد.
CAH به زاویه تتا، وتر احتیاج داره که اینارو میدونین، و همچنین سمت موافق که اونو نمیدونین، پس کوسینوس هم تابع مثلثاتی درست نیست.
۳. تابع انتخاب شده رو بسط بدین، مقدار نامشخص رو منزوی کنید و حل کنید.
میدونین که کوسینوس تتا موسوی سمت مجاور تقسیم بر وتره و مقدار نامشخص، سمت مجاوره، پس باید منزویش کنیم:
سمت مجاور = کوسینوس تتا ضرب در وتر = کوسینوس ۷۴ درجه ضرب در ۱۵ متر
خوب حالا ماشین حسابتونو در بیارید و ۷۴ رو بزنین توش و دکمه کوسینوس رو بزنید. مقدارش ۰/۲۷۵۶ که باید اونو گرد کنید به ۰/۲۸.
مطمئن باشد که ماشین حساب داره حالت زاویه ای درست رو حساب میکنه. بیشتر ماشین حساب ها هم درجه رو حساب میکنند و هم رادیان. وقتی دکمه MODE رو میزنید، بهتون میگه که داره درجه رو حساب میکنه یا رادیان. مقدار کوسینوس ۷۴ درجه رو توی فرمول قرار بدید:
سمت مجاور = ۰/۲۸ ضرب در ۱۵ متر = ۴/۲ متر
طول سمت مجاور، ۴/۲ متره.
برای محاسبه سمت مخالف، مرحله های مشابه رو طی کنید:
۱- مقادیر معلوم رو مشخص و جدول متغیر هارو درست کنی.
تتا = ۷۴ درجه
وتر (H) = پانزده متر
سمت مخالف = نا معلوم
۲. تابع مثلثاتی برای استفاده رو مشخص کنید.
اول، SOH CAH TOA رو به یاد بیارید و تابع مناسب رو انتخاب کنید.
SOH به زاویه تتا و وتر احتیاج داره که شما میدونید و همچنین سمت مخالف که نمیدونید. پس سینوس، تابع مورد نظره.
۳. تابع انتخاب شده رو بسط بدین، مقدار نامشخص رو منزوی کنید و حل کنید.
میدونین که سینوس تتا = سمت مخالف تقسیم بر وتر، و مقدار نامعلوم، سمت مخالفه، پس باید منزویش کنید:
سمت مخالف = سینوس تتا ضرب در وتر = سینوس ۷۴ درجه ضرب در ۱۵ متر = ۰/۹۶ ضرب در ۱۵ متر = ۱۴/۴ متر
طول سمت مخالف. ۱۴/۴ متره.
میتونین چک کنید که طول هایی که حساب کردین، درستن یا نه. کافیه بذاریدشون توی قضیه فیثاغورس A2 + O2 = H2
۴/۲ به توان ۲ + ۱۴/۴ به توان ۲ = ۱۵ به توان ۲
۱۷/۶ + ۲۰۷/۴ = ۲۲۵
۲۲۵ = ۲۲۵
نامگذاری درست سمت های مثلث قائم الزاویه مهمه. اگه برعکس باشن، اندازه ها درست میشن اما به سمت های متفاوت ربط پیدا میکنن.
توی بیومکانیک، تابع تانژانت کمتر از سینوس و کوسینوس استفاده میشه. دیگه مثالشو نمیزنم اما روندش مثل سنون و کوسینوسه.
استفاده از آرک تانژانت برای حل کردن زاویه تتا
بعضی وقتا، شما مقدار سمت مجاور و مخالف رو میدونین، اما مقدار وتر و زاویه تتا رو نمیدونین. تو شکل ۴-۲ یه نمونه رو میبینید.
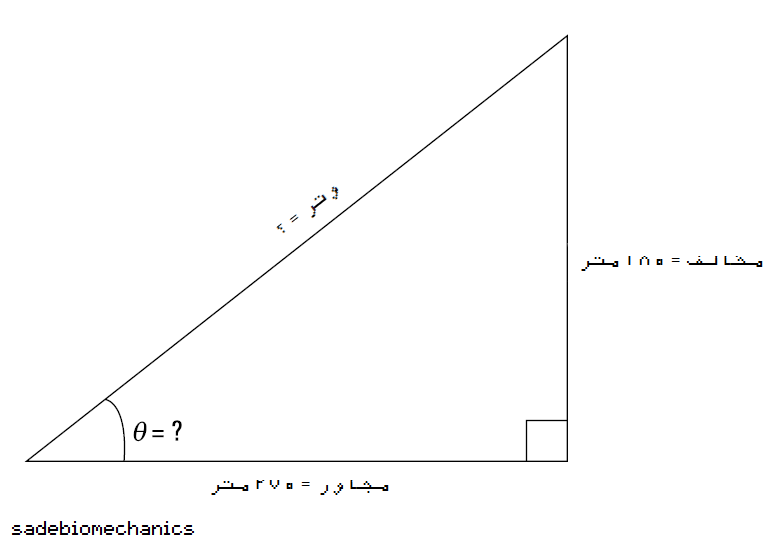
تو این مثال، میتونین طول وتر رو با قضیه فیثاغورس حساب کنید