۲/۹ - رام کردن مقادیر برداری

مقدار، چیزی است که بشه اندازه اش گرفت. توی بیومکانیک، دو نوع مقدار، مهم هستن:

عددی: یه مقدار عددی، هر چیزیه که بشه با قدر، اندازه یا مقدارش توضیحش داد. مقادیر عددی شامل زمان، جرم، فاصله و اسپید هستن. یه عدد خاص برای اندازه گیری هر واحد، استفاده میشه. مثلا زمان = ۸ ثانیه (یا s)، جرم = ۷۵ kg، فاصله = ۲ m، یا اسپید = ۲۰ متر بر ثانیه (m/s).

برداری: یه مقدار برداری رو فقط با قدر و جهتی که با ان مقدار مرتبطه اندازه میگیرن. مقادیر برداری شامل، نیرو، جابجایی، سرعت و شتاب میشن. مثلا، نیرو = ۲۰ نیوتون (یا N)، سرعت = ۵ متر بر ثانیه در زاویه ای ۲۰ درجه ای، یا شتاب = ۱۰ متر بر مجذور ثانیه به سمت پایین.

یه مقدار برداری رو با یه فلش نشون میدن. مقدار بردار، طولشه و جهتش هم از نوک بردار مشخص میشه. 

۲/۸ - حقه های مثلثاتی

مثلثات یک رشته از ریاضی است که رابطه بین طرف و زاویه مثلثات را شرح میده. مثل قضیه فیثاغورس، بهتون اجازه میده تا طول نا معلوم یک مثلث قائم الزاویه رو حساب کنید. توابع مثلثاتی، جعبه ابزار شما برای کار با مثلث های قایم الزاویه هستند. 

۲/۷ - استفاده از قضیه فیثاغورس

قضیه فیثاغورس، طول سه سمت یک مثلث قائم الزاویه رو به هم مرتبط میکنه. با استفاده از اسامی که استفاده شده از شکل ۲-۲، این قضیه رو این شکلی مینویسیم: مجاور به توان ۲ به اضافه مخالف به توان ۲ مساوی با وتر است یا O2 + A2 = H2 

قضیه فیثاغورس برای همه مثلث های قائم الزاویه صدق میکند.

فرم آشنای  قضیه فیثاغورس به صورت a2 + b2 = c2 است. 

۲/۶ - گشتن دنبال وتر

چند اصول اساسی هندسه توی بیومکانیک به کار میرن. مثلث قائم الزاویه، شکلی مهم توی حل کردن مسائل بیومکانیکه، چون رابطه بین طول ها میتونه توی کار با بردار ها کمک کننده باشه.

شکل ۲-۲ یه مثلث قائم الزاویه رو نشون میده، که یکی از زاویه هاش ۹۰ درجه ست که با یه مربع کوچیک تو اون زاویه مشخص میشه.

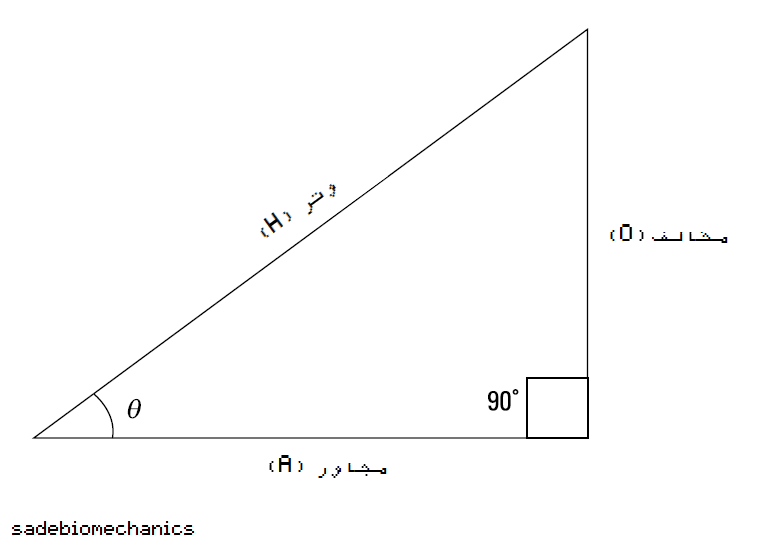
سمت روبروی زاویه ۹۰ درجه، وتر نام داره که همیشه بلندترین سمت مثلثه.

تو همه مثلث ها، جمع زوایا، ۱۸۰ درجه است. پس جمع دو زاویه دیگه توی مثلث قائم الزاویه، ۹۰ درجه است. زاویه کمتر از ۹۰ درجه، حاد نام داره.

تو شکل ۲-۲، یکی از زاویه های حاد، به عنوان مرجع انتخاب شده که با علامت یونانی تتا مشخص شده. سمت روبروی تتا، مخالف نامیده میشه و سمت بغل تتا، مجاور.

قدم اولیه برای انتخاب یکی از زوایا به عنوان مرجع و نامیدن سمت مجاور و مخالف، قدم مهمی برای حل مسائل بیومکانیکه. وتر هیچ وقت تغییر نمیکنه، ولی سمت مجاور و مخالف میتونه تغییر کنه و بستگی داره که تتا رو کجا انتخاب کنید.

۲/۵ - تفسیر متناسب

توی ریاضی، متغیر ها متناسب با هم تغییر میکنن. بنابرین دو تا قانون تفسیر متناسب اینا هستن:

وقتی زیاد شدن یک متغیر سبب زیاد شدن دیگری میشه، متغیر ها مستقیما متناسب اند و این جوری نوشته میشه y = x. اگه x مقدارش ۲ باشه، y هم ۲ هست.

وقتی زیاد شدن یک متغیر، سبب کاهش یک متغیر میشه، این دو تا به صورت عکس، متناسب اند و معمولا به صورت y = 1 / x نوشته میشه. اگه x مساوی ۲ باشه، y مقدارش، نیم هست.

فرمول F = ma رو در نظر بگیرید (بیانیه ساده یکی از قوانین مکانیک که به قانون دوم نیوتون معروفه و توی فصل ۶ در موردش حرف میزنیم). با منزوی کردن a، فرمول این شکلی میشه: 

a = F / m

مفاهیم سمت راست فرمول (F و m) متناسب با a هستند و هردوشون، اندازه a رو تحت تاثیر قرار میدن.

با استفاده از قوانین بالا، a مستقیما متناسبه با F. اگه m یه مقدار ثابت باشه (مثلا ۱۰)، اگه F بزرگ تر بشه، a هم بزرگتر میشه. اگه F مقدارش ۲۰ باشه، اون وقت a هم ۲ هست. اگه F، سی باشه، اون وقت a هم ۳ هست.

در مقابل، a به صورت برعکس با m متناسبه. اگه F ثابت باشه (مثلا ۱۰۰)، اگه m بزرگ شه، a کم میشه. اگه m مساوی ۲۰ باشه، a برابر ۵ هست و اگه m مقدارش ۱۰۰ باشه، اون وقت m هم ۱ میشه.